Solving a simple puzzle using SymPy
I came across this problem recently:
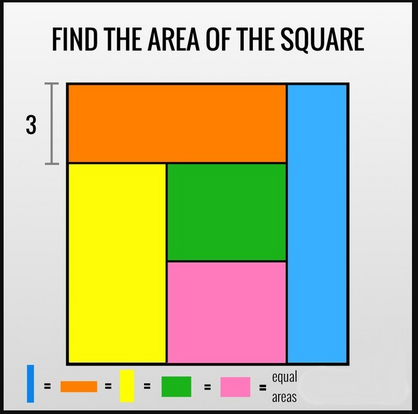
It’s about a square that gets partitioned into rectangles of equal area (some sources call this "floorplan" ).
One of the sides of these smaller rectangles is given and the problem asks for the area of the large square.
It’s possible to build equations for:
the known side of the small rectangle
the smaller rectangle sides that add up to the same length of the large square side-length
the areas of the smaller rectangles being equal
I thought of writing them out by hand but then realized it would be possible to just generate the equations (even if some of them might be redundant).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# o,y,p,b,g
from sympy import *
ow,oh,yw,yh,pw,ph,bw,bh,gw,gh = symbols('o_w o_h y_w y_h p_w p_h b_w b_h g_w g_h')
u1 = ow+bw
u2 = yw+pw+bw
u3 = oh+yh
u4 = bh
u5 = oh+gh+ph
u6 = yw+gw+bw
P = [ow*oh,yw*yh,pw*ph,bw*bh,gw*gh]
U=[u1,u2,u3,u4,u5,u6]
l=len(U)
E=[]
E.append(Eq(oh,3))
for i in range(l):
for j in range(i):
e = U[i]-U[j]
E.append(Eq(e,0))
l=len(P)
for i in range(l):
for j in range(i):
e = P[i]-P[j]
E.append(Eq(e,0))
S = solve(E)
print(S)
L = 3 + S[0][yh]
print("L=",L)
This will build a system of equations which is then passed to SymPy.
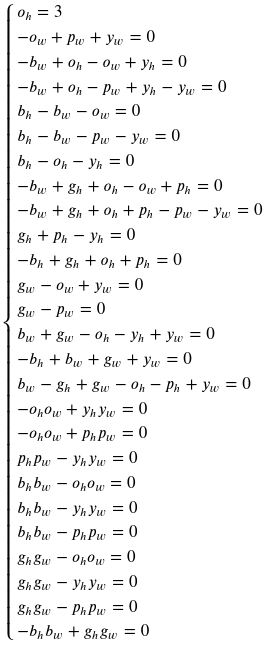
After it’s solved, we can get the side of the square by adding 3 to the yellow height.